SciPy) 자주 사용하는 기능들 - 거리

 

1. 두 지점에 대한pair-wise distance

from scipy.spatial.distance import pdist
points = [[0, 0], [1, 1], [2, 2]]
print(pdist(points))  # 유클리드 거리

2. 두 집합에 대한 pair-wise distance

from scipy.spatial.distance import cdist
print(cdist([[0, 0]], [[1, 1], [2, 2]]))

3. 유클리드 거리(L2)

from scipy.spatial.distance import euclidean
print(euclidean([0, 0], [3, 4]))  # 결과: 5.0

4. L1 거리

from scipy.spatial.distance import cityblock
print(cityblock([1, 2], [3, 4]))

5. 코사인 유사도 거리

from scipy.spatial.distance import cosine
print(cosine([1, 0], [0, 1]))  # 결과: 1.0 (완전 비슷)

6. correlaton 기반 거리

from scipy.spatial.distance import correlation
print(correlation([1, 2, 3], [4, 5, 6]))

7. 체비셰프 거리

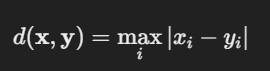
from scipy.spatial.distance import chebyshev
print(chebyshev([0, 0], [3, 4]))

8. 자카드 거리

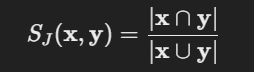
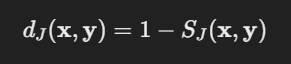
from scipy.spatial.distance import jaccard

x = [1, 0, 1, 1, 0]
y = [0, 1, 1, 1, 0]

dist = jaccard(x, y)
print("Jaccard Distance:", dist)

 

교집합 : [1,0,1,1,0] ∩ [0,1,1,1,0]=[0,0,1,1,0] -> 2개

합집합 : [1,0,1,1,0]∪[0,1,1,1,0]=[1,1,1,1,0] -> 4개

-> 지금 교집합, 합집합이 엄밀히 말해 집합을 대상으로 하고있진 않다. 

-> 순서대로 매칭했을 때, 둘이 같으면 1, 같지 않으면 0을 반환하는 연산이라고 보면 된다.

-> 그 중, 자카드 유사도는 최종 결과에 1이 몇 개 들어있는지

(즉, 비교하는 두 대상 각각의 요소에 얼마나 같은게 있는지)를 계산한다.

 

자카드 유사도 = 2/4 = 0.5

자카드 거리 = 1 - 0.5 = 0.5

9. 민코프스키 거리

from scipy.spatial.distance import minkowski
print(minkowski([1, 2], [3, 4], p=3))

10. 가중 민코프스키 거리

from scipy.spatial.distance import wminkowski
print(wminkowski([1, 2], [3, 4], p=2, w=[0.5, 0.5]))

 

---

11. 마할라노비스 거리(공분산 고려)

from scipy.spatial.distance import mahalanobis
import numpy as np

A = np.array([[1, 2], [3, 4]])
B = np.array([[2, 3], [4, 5]])
VI = np.linalg.inv(np.cov(A.T))  # 공분산 행렬의 역행렬

mahal_dist = mahalanobis(A[0], B[0], VI)
print("Mahalanobis Distance:", mahal_dist)

 

12. Frobenius Norm

import numpy as np

A = np.array([[1, 2], [3, 4]])
B = np.array([[2, 3], [4, 5]])

frobenius_dist = np.linalg.norm(A - B, 'fro')
print("Frobenius Distance:", frobenius_dist)

 

13. Spectral Norm

 

행렬 A, B의 고유값의 최대값을 기준으로 거리 측정

spectral_dist = np.linalg.norm(A - B, 2)  # 2는 스펙트럴 노름
print("Spectral Distance:", spectral_dist)

14. Trace Norm

 

 

행렬의 차이에 대한 singular value의 합을 거리로 측정

trace_dist = np.linalg.norm(A - B, 'nuc')  # 'nuc'는 핵 노름
print("Trace Norm Distance:", trace_dist)

15. Bures Wasserstein Distance

 

Positive Definite matrix간의 거리.

행렬의 구조적 유사성 반영.

P.D만 입력 가능

from scipy.linalg import sqrtm
A = np.array([[4, 1], [1, 3]])
B = np.array([[3, 0], [0, 2]])

# 거리 계산
dist = np.linalg.norm(sqrtm(A) - sqrtm(B), 'fro')
print("Bures-Wasserstein Distance:", dist)

16. Operator Norm

 

행렬을 선형 변환으로 간주하고, 변환 효과간 차이를 측정.

op_norm = np.linalg.norm(A - B, ord=2)  # 연산자 노름
print("Operator Norm Distance:", op_norm)